Optimal control for robotics is a powerful tool to synhesize motions and controls through task goals (cost/optimality) and constraints (e.g., system dynamics, interaction constraints). It aims to achieve complex motor maneuvers in real-time while formally considering its intrinsic properties: nonholonomics, actuation limits, balance, kinematic range, etc. Solving optimal control problems efficiently require (i) to exploit the temporal and functional structure and (ii) to develop numerical optimization algorithms with great convergence rate and computational speed. Our lab is committed to enhance the numerical capabilities of optimal control algorithms and share our methods to the robotics community as part of our Crocoddyl open-source library.
Crocoddyl (Contact RObot COntrol by Differential DYnamic Library) is an open-source framework tailored for efficient multi-contact optimal control. Crocoddyl efficiently computes the state trajectory and the control policy for a given predefined sequence of contacts. Its efficiency is due to the use of sparse analytical derivatives, exploitation of the problem structure, and data sharing. It employs differential geometry to properly describe the state of any geometrical system, e.g. floating-base systems such as humanoid and quadruped robots.
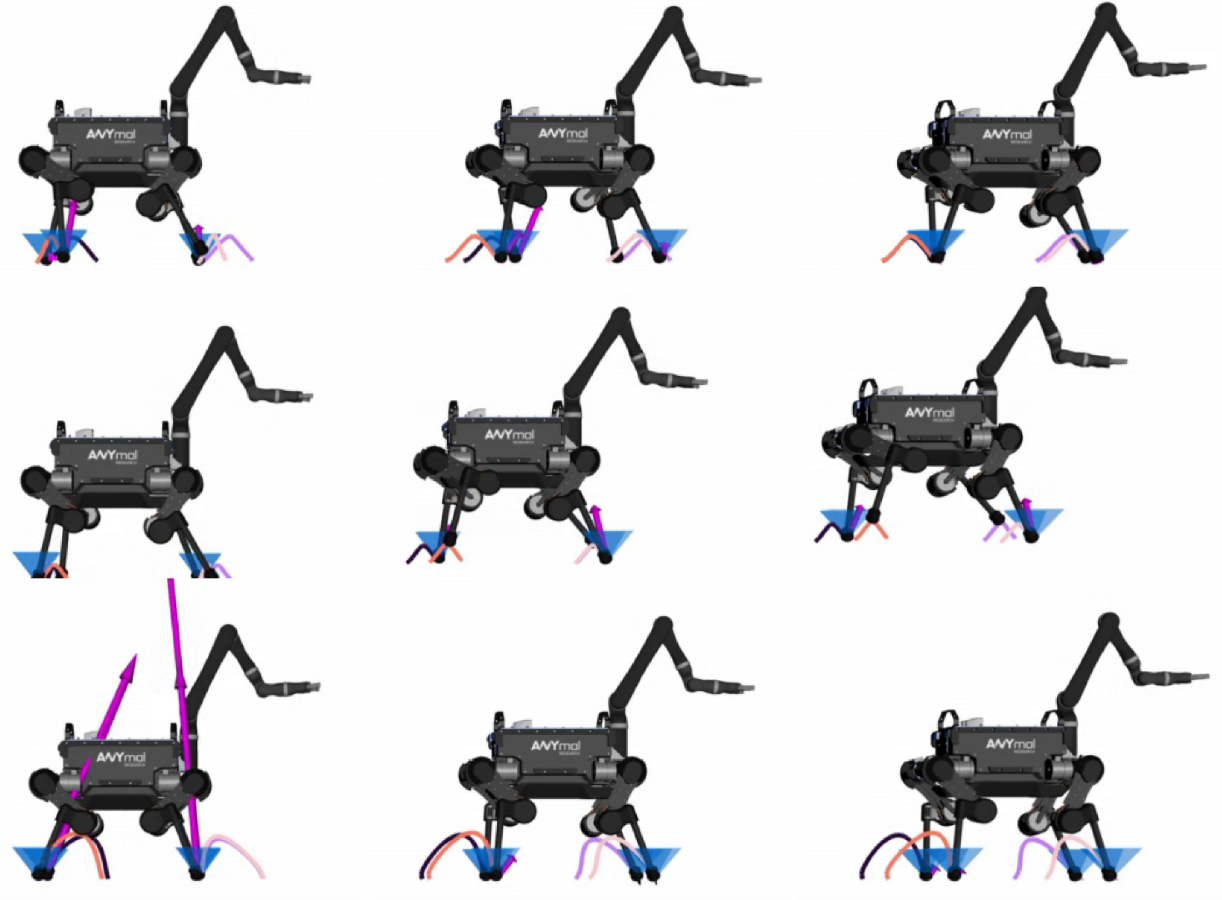
We also propose a novel multiple-shooting method called feasibility-driven differential dynamic programming (FDDP). FDDP has a greater globalization strategy compared to the classical DDP algorithm as it behaves similarly to multiple-shooting methods with only equality constraints. With the FDDP algorithm, we can compute highly-dynamic maneuvers for legged robots (e.g. jumping, front-flip) in the order of milliseconds.
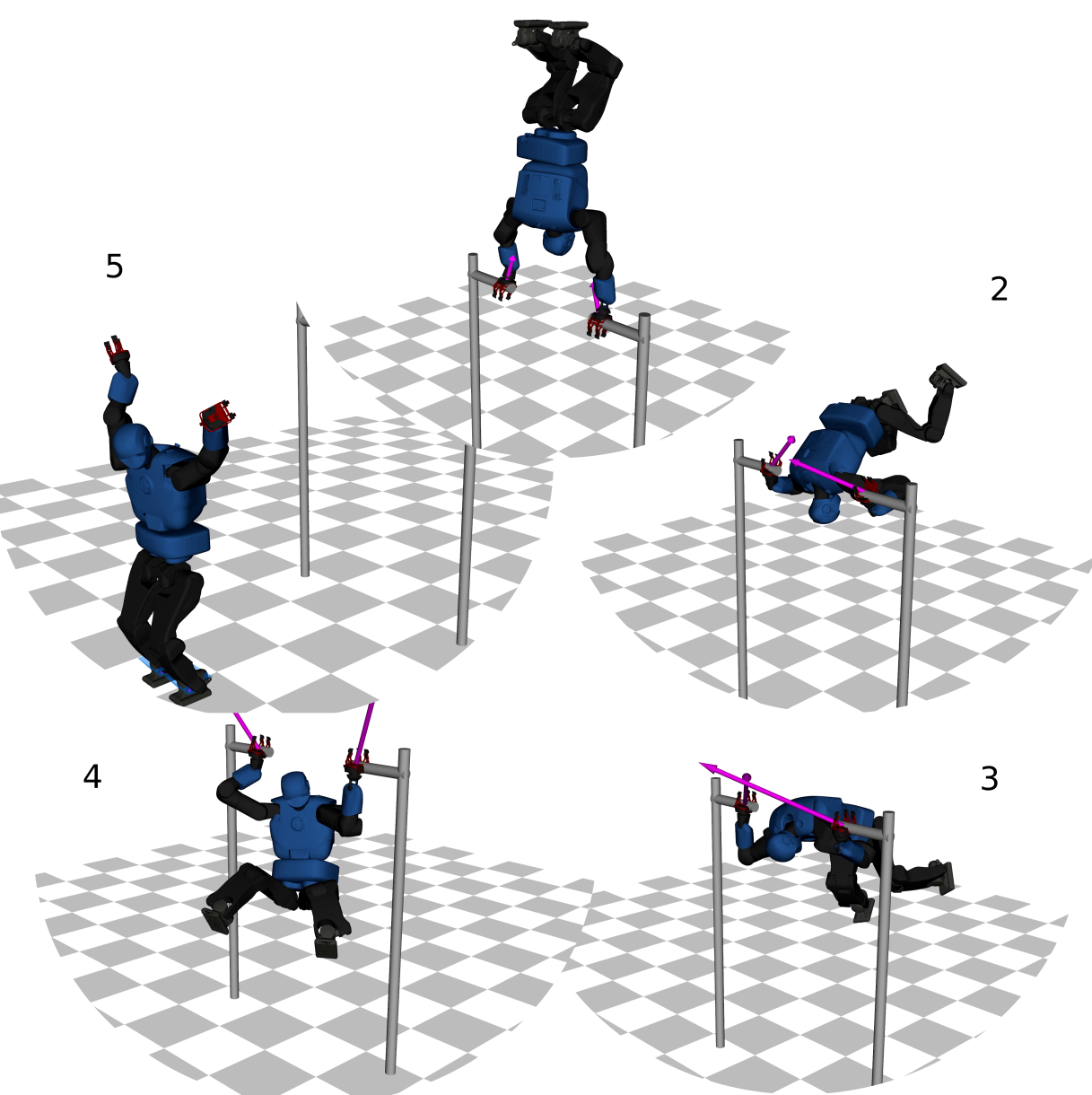
Optimal control using inverse dynamics provides different numerical benefits such as coarse optimization, cheaper computation of derivatives, and higher convergence rate. However, to achieve the same level of computation efficiency obtained in forward dynamics formulations, it is crucial to handle equality constraints without increasing the algorithm complexity and to exploit its temporal and functional structure. With temporal structure, we refer to the inherent Markovian dynamics commonly encountered in optimal control problems. Instead, with functional structure, we refer to the sparsity pattern defined by the inverse dynamics itself.
To this aim, we propose a novel approach to handle equality constraints based on null-space parametrization. Our approach balances optimality in both dynamics and equality-constraint feasibility appropriately. This is a critical aspect to increase the algorithm globalization needed to compute agile or complex motions. Furthermore, we introduce a condensed formulation using inverse dynamics that considers arbitrary actuator models.
Robot Motor Intelligence (RoMI) Lab
We are part of the National Robotarium and the Edinburgh Centre for Robotics at Heriot-Watt University.
Contact:
© Robot Motor Intelligence (RoMI) Lab, 2023