We present an approach to differentiable optimal control with applications to robot design optimization (co-design), imitation learning and system identification. We propose three techniques for differentiating the optimal control problem. Firstly, we present a fully exact approach that differentiates the differential dynamic programming (DDP) algorithm based on sensitivity analysis (SA). We validate the numerical correctness of this approach on the pendulum and double pendulum systems and scale it up to the Kinova robotic arm. However, for more complex systems such as legged robots, some of the components of this derivative are not yet available or prohibitively slow to compute. In this case, we present two approaches that use finite differences in parts or for the whole derivative of the optimal control problem via DDP. To show the real-world use of our approach, we develop an interactive co-design tool for quadrupeds that allows for rapid evaluation of robot designs and also presents hardware results on the quadruped Solo. We further compare our approach to a nonlinear programming approach and show a 54-times improvement in computational speed.


Achieving agile maneuvers through multiple contact phases has been a longstanding challenge in legged robotics. It requires to derive motion plans and local control feedback policies in real-time to handle the nonholonomy of the kinetic momenta. While a few recent predictive control approaches based on centroidal momentum have been able to generate dynamic motions, they assume unlimited actuation capabilities. This assumption is quite restrictive and does not hold for agile maneuvers on most robots. In this work, we present a contact-phase predictive and state-feedback controllers that enables legged robots to plan and perform agile locomotion skills. Our predictive controller models the contact phases using a hybrid paradigm that considers the robot's actuation limits and full dynamics. We demonstrate the benefits of our approach on agile maneuvers on ANYmal robots in realistic scenarios. To the best of our knowledge, our work is the first to show that predictive control can handle actuation limits, generate agile locomotion maneuvers and execute locally optimal feedback policies on hardware without the use of a separate whole-body controller.

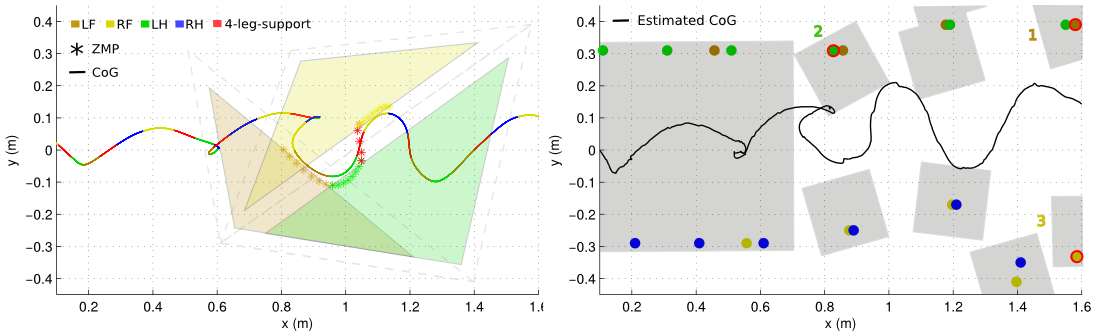
Optimal estimation is a promising tool for estimation of payloads' inertial parameters and localization of robots in the presence of multiple contacts. To harness its advantages in robotics, it is crucial to solve these large and challenging optimization problems efficiently. To tackle this, we (i) develop a multiple shooting solver that exploits both temporal and parametric structures through a parametrized Riccati recursion. Additionally, we (ii) propose an inertial manifold that ensures the full physical consistency of inertial parameters and enhances convergence. To handle its manifold singularities, we (iii) introduce a nullspace approach in our optimal estimation solver. Finally, we (iv) develop the analytical derivatives of contact dynamics for both inertial parametrizations. Our framework can successfully solve estimation problems for complex maneuvers such as brachiation in humanoids, achieving higher accuracy than conventional least squares approaches. We demonstrate its numerical capabilities across various robotics tasks and its benefits in experimental trials with the Go1 robot.



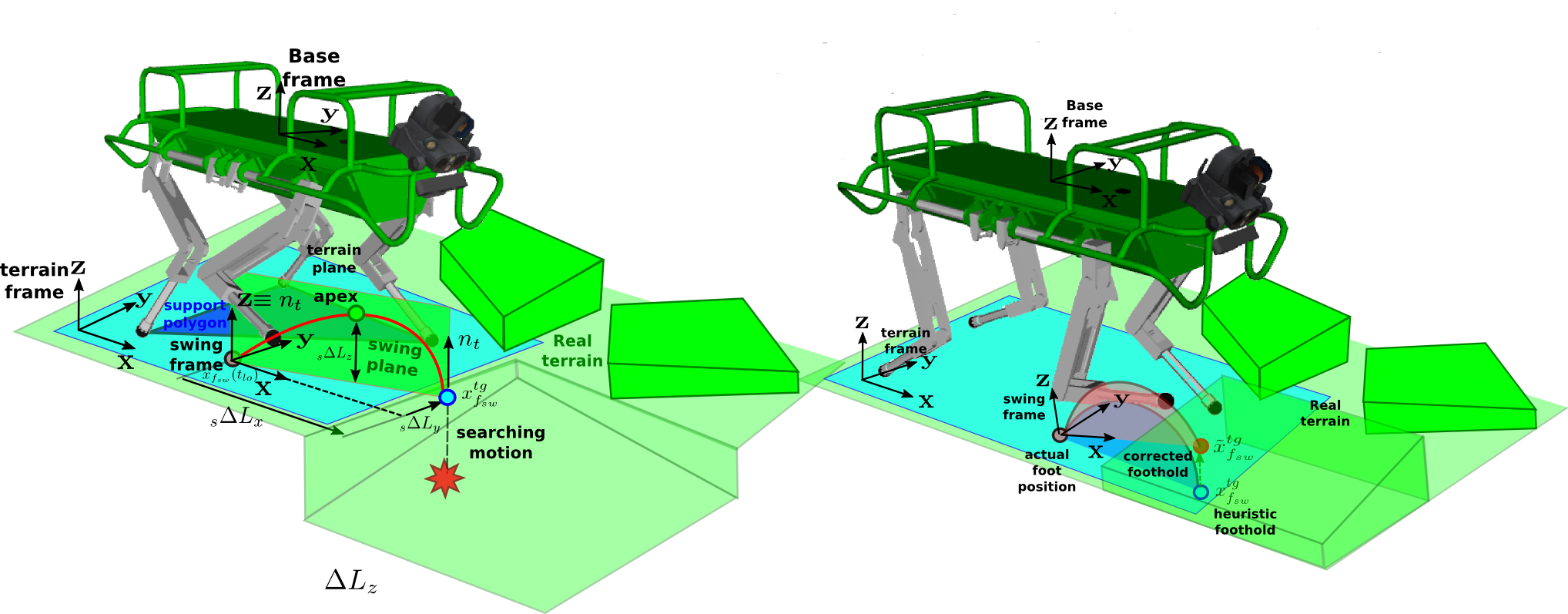
Real-time synthesis of legged locomotion maneuvers in challenging industrial settings is still an open problem, requiring simultaneous determination of footsteps locations several steps ahead while generating whole-body motions close to the robot's limits. State estimation and perception errors impose the practical constraint of fast re-planning motions in a model predictive control (MPC) framework. We first observe that the computational limitation of perceptive locomotion pipelines lies in the combinatorics of contact surface selection. Re-planning contact locations on selected surfaces can be accomplished at MPC frequencies (50-100 Hz). Then, whole-body motion generation typically follows a reference trajectory for the robot base to facilitate convergence. We propose removing this constraint to robustly address unforeseen events such as contact slipping, by leveraging a state-of-the-art whole-body MPC (Croccodyl). Our contributions are integrated into a complete framework for perceptive locomotion, validated under diverse terrain conditions, and demonstrated in challenging trials that push the robot's actuation limits, as well as in the ICRA 2023 quadruped challenge simulation.


We introduce a novel method for handling endpoint constraints in constrained differential dynamic programming (DDP). Unlike existing approaches, our method guarantees quadratic convergence and is exact, effectively managing rank deficiencies in both endpoint and stagewise equality constraints. It is applicable to both forward and inverse dynamics formulations, making it particularly well-suited for model predictive control (MPC) applications and for accelerating optimal control (OC) solvers. We demonstrate the efficacy of our approach across a broad range of robotics problems and provide a user-friendly open-source implementation within CROCODDYL.


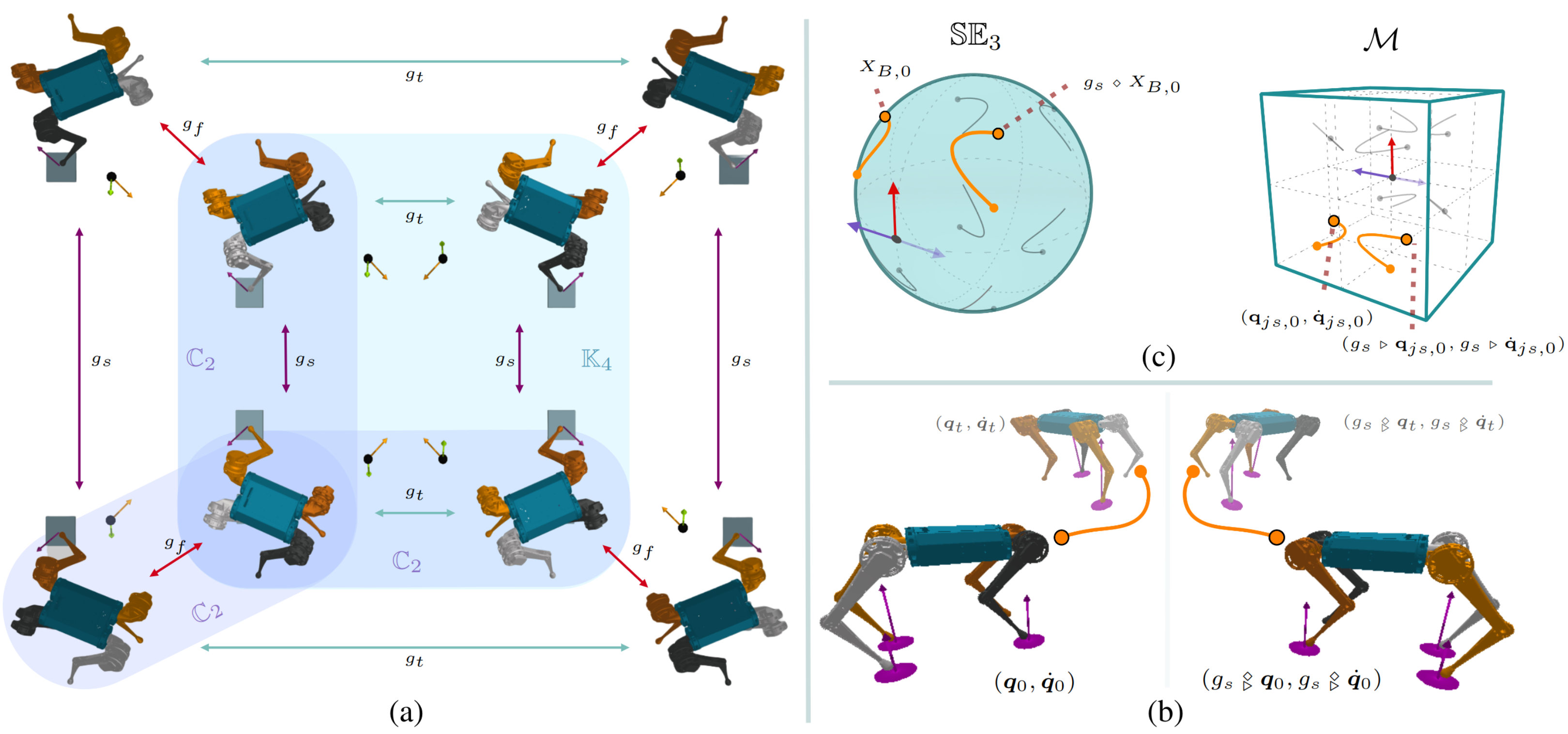
We present a comprehensive framework for studying and leveraging morphological symmetries in robotic systems. These are intrinsic properties of the robot’s morphology, frequently observed in animal biology and robotics, which stem from the replication of kinematic structures and the symmetrical distribution of mass. We illustrate how these symmetries extend to the robot’s state space and both proprioceptive and exteroceptive sensor measurements, resulting in the equivariance of the robot’s equations of motion and optimal control policies. Thus, we recognize morphological symmetries as a relevant and previously unexplored physics-informed geometric prior, with significant implications for both data-driven and analytical methods used in modeling, control, estimation and design in robotics. For data-driven methods, we demonstrate that morphological symmetries can enhance the sample efficiency and generalization of machine learning models through data augmentation, or by applying equivariant/invariant constraints on the model’s architecture. In the context of analytical methods, we employ abstract harmonic analysis to decompose the robot’s dynamics into a superposition of lower-dimensional, independent dynamics. We substantiate our claims with both synthetic and real-world experiments conducted on bipedal and quadrupedal robots. Lastly, we introduce the repository MORPHOSYMM to facilitate the practical use of the theory and applications outlined in this work.

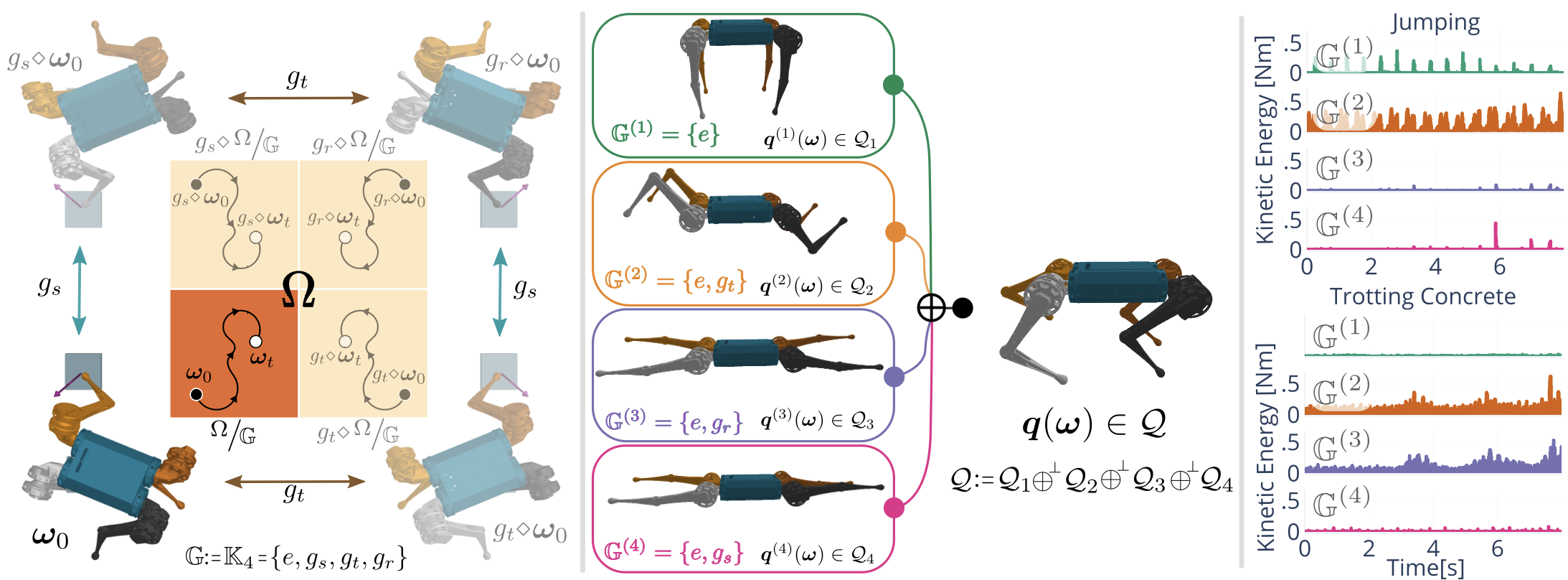
We introduce the use of harmonic analysis to decompose the state space of symmetric robotic systems into orthogonal isotypic subspaces. These are lower-dimensional spaces that capture distinct, symmetric, and synergistic motions. For linear dynamics, we characterize how this decomposition leads to a subdivision of the dynamics into independent linear systems on each subspace, a property we term dynamics harmonic analysis (DHA). To exploit this property, we use Koopman operator theory to propose an equivariant deep-learning architecture that leverages the properties of DHA to learn a global linear model of system dynamics. Our architecture, validated on synthetic systems and the dynamics of locomotion of a quadrupedal robot, demonstrates enhanced generalization, sample efficiency, and interpretability, with less trainable parameters and computational costs.


Full-dynamics model predictive control (MPC) has recently been applied to quadrupedal locomotion in semi-unstructured environments. These advances have been fueled by the availability of efficient trajectory optimization (TO) algorithms and inexpensive computational power. The main advantages of full-dynamics MPC are (i) enabling complex locomotion manoeuvres, (ii) considering actuation limits, and (iii) improving robot stability. However, to make the TO problem sufficiently simple to be solved at run time, reference swing foot trajectories are usually tracked in the MPC formulation. These trajectories are often computed independently of the motion of the joints, limiting the approach generality and capability. To address this limitation, we present a full-dynamics MPC formulation that does not require reference swing-foot trajectories, featuring a novel cost function targeting swing foot motion and considering environmental information. Removing the need for reference swing foot trajectories, our approach can also automatically adjust footstep locations, as long as the contact surfaces are predefined. We have validated our MPC formulation through simulations and experiments on the ANYmal B robot. Our approach has similar computational efficiency to state-of-the-art formulations, while displaying superior push-recovery capabilities on various terrains.



Optimal control (OC) using inverse dynamics pro- vides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. How- ever, to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle efficiently its large number of equality constraints. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to high- quality local minima. To do so, we (ii) modify our feasibility- driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of inverse dynamics that considers arbitrary actuator models. We also propose (iv) a novel MPC based on inverse dynamics within a perceptive locomotion framework. Finally, we present (v) a theoretical com- parison of optimal control with forward and inverse dynamics and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and gen- erate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.



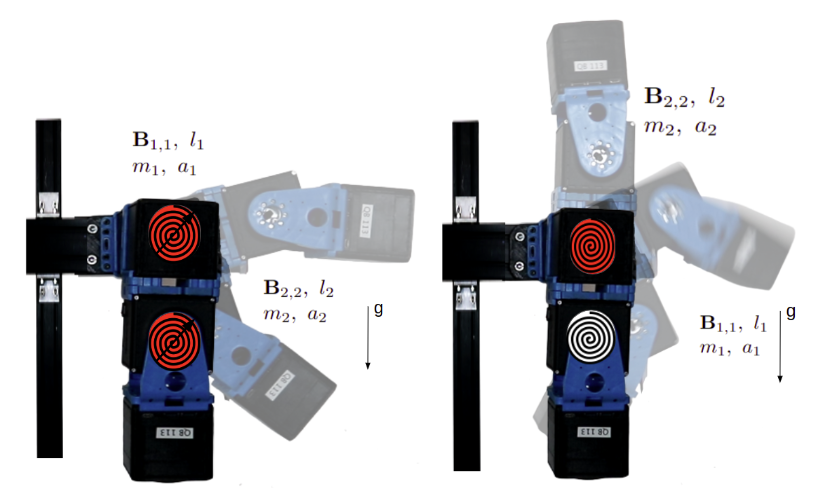
Soft robots can execute tasks with safer interactions. However, control techniques that can effectively exploit the systems' capabilities are still missing. Differential dynamic programming (DDP) has emerged as a promising tool for achieving highly dynamic tasks. But most of the literature deals with applying DDP to articulated soft robots by using numerical differentiation, in addition to using pure feed-forward control to perform explosive tasks. Further, underactuated compliant robots are known to be difficult to control and the use of DDP-based algorithms to control them is not yet addressed. We propose an efficient DDP-based algorithm for trajectory optimization of articulated soft robots that can optimize the state trajectory, input torques, and stiffness profile. We provide an efficient method to compute the forward dynamics and the analytical derivatives of series elastic actuators (SEA)/variable stiffness actuators (VSA) and underactuated compliant robots. We present a state-feedback controller that uses locally optimal feedback policies obtained from DDP. We show through simulations and experiments that the use of feedback is crucial in improving the performance and stabilization properties of various tasks. We also show that the proposed method can be used to plan and control underactuated compliant robots, with varying degrees of underactuation} effectively.



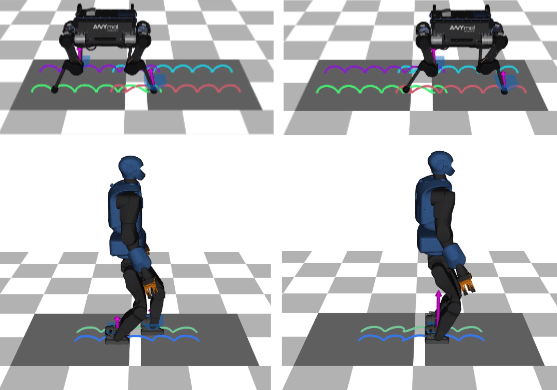
State-of-the-art approaches to footstep planning assume reduced-order dynamics when solving the combinatorial problem of selecting contact surfaces in real time. However, in exchange for computational efficiency, these approaches ignore joint torque limits and limb dynamics. In this work, we address these limitations by presenting a topology-based approach that enables model predictive control (MPC) to simultaneously plan full-body motions, torque commands, footstep placements, and contact surfaces in real time. To determine if a robot's foot is inside a contact surface, we borrow the winding number concept from topology. We then use this winding number and potential field to create a contact-surface penalty function. By using this penalty function, MPC can select a contact surface from all candidate surfaces in the vicinity and determine footstep placements within it. We demonstrate the benefits of our approach by showing the impact of considering full-body dynamics, which includes joint torque limits and limb dynamics, on the selection of footstep placements and contact surfaces. Furthermore, we validate the feasibility of deploying our topology-based approach in an MPC scheme and explore its potential capabilities through a series of experimental and simulation trials.



Differential dynamic programming (DDP) is a direct single shooting method for trajectory optimization. Its efficiency derives from the exploitation of temporal structure (inherent to optimal control problems) and explicit roll-out/integration of the system dynamics. However, it suffers from numerical instability and, when compared to direct multiple shooting methods, it has limited initialization options (allows initialization of controls, but not of states) and lacks proper handling of control constraints. In this work, we tackle these issues with a feasibility-driven approach that regulates the dynamic feasibility during the numerical optimization and ensures control limits. Our feasibility search emulates the numerical resolution of a direct multiple shooting problem with only dynamics constraints. We show that our approach (named BOX-FDDP) has better numerical convergence than BOX-DDP+ (a single shooting method), and that its convergence rate and runtime performance are competitive with state-of-the-art direct transcription formulations solved using the interior point and active set algorithms available in KNITRO. We further show that BOX-FDDP decreases the dynamic feasibility error monotonically—as in state-of-the-art nonlinear programming algorithms. We demonstrate the benefits of our approach by generating complex and athletic motions for quadruped and humanoid robots. Finally, we highlight that BOX-FDDP is suitable for model predictive control in legged robots.


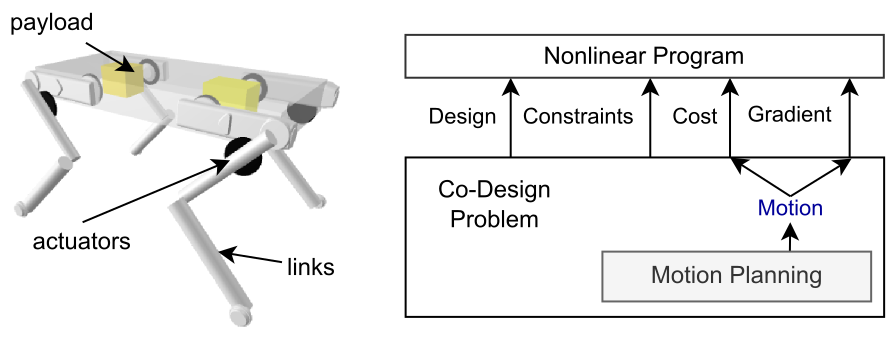
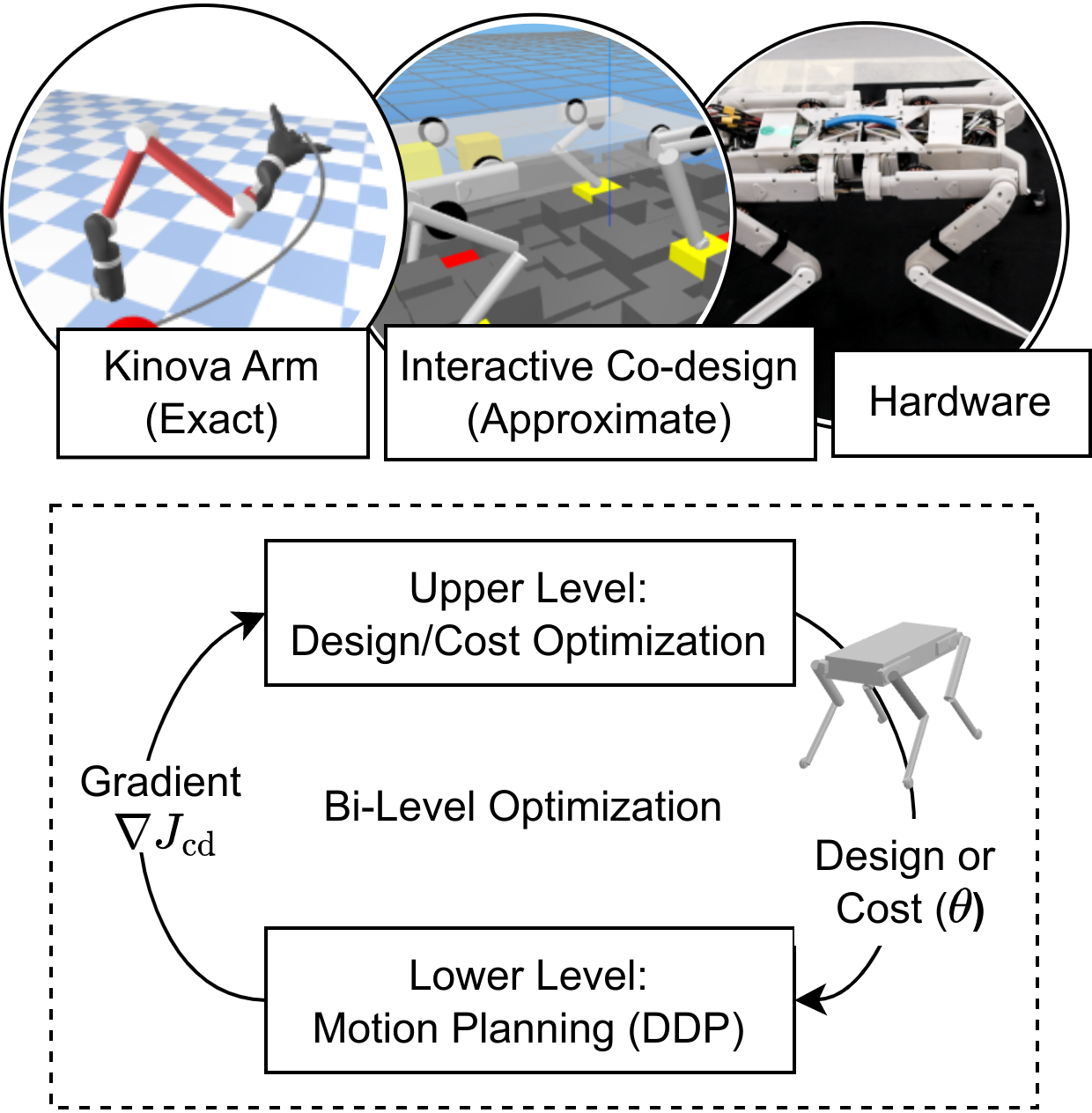
We present a versatile framework for the computational co-design of legged robots and dynamic maneuvers. Current state-of-the-art approaches are typically based on random sampling or concurrent optimization. We propose a novel bilevel optimization approach that exploits the derivatives of the motion planning sub-problem (i.e., the lower level). These motion-planning derivatives allow us to incorporate arbitrary design constraints and costs in an general-purpose nonlinear program (i.e., the upper level). Our approach allows for the use of any differentiable motion planner in the lower level and also allows for an upper level that captures arbitrary design constraints and costs. It efficiently optimizes the robot's morphology, payload distribution and actuator parameters while considering its full dynamics, joint limits and physical constraints such as friction cones. We demonstrate these capabilities by designing quadruped robots that jump and trot. We show that our method is able to design a more energy-efficient Solo robot for these tasks.


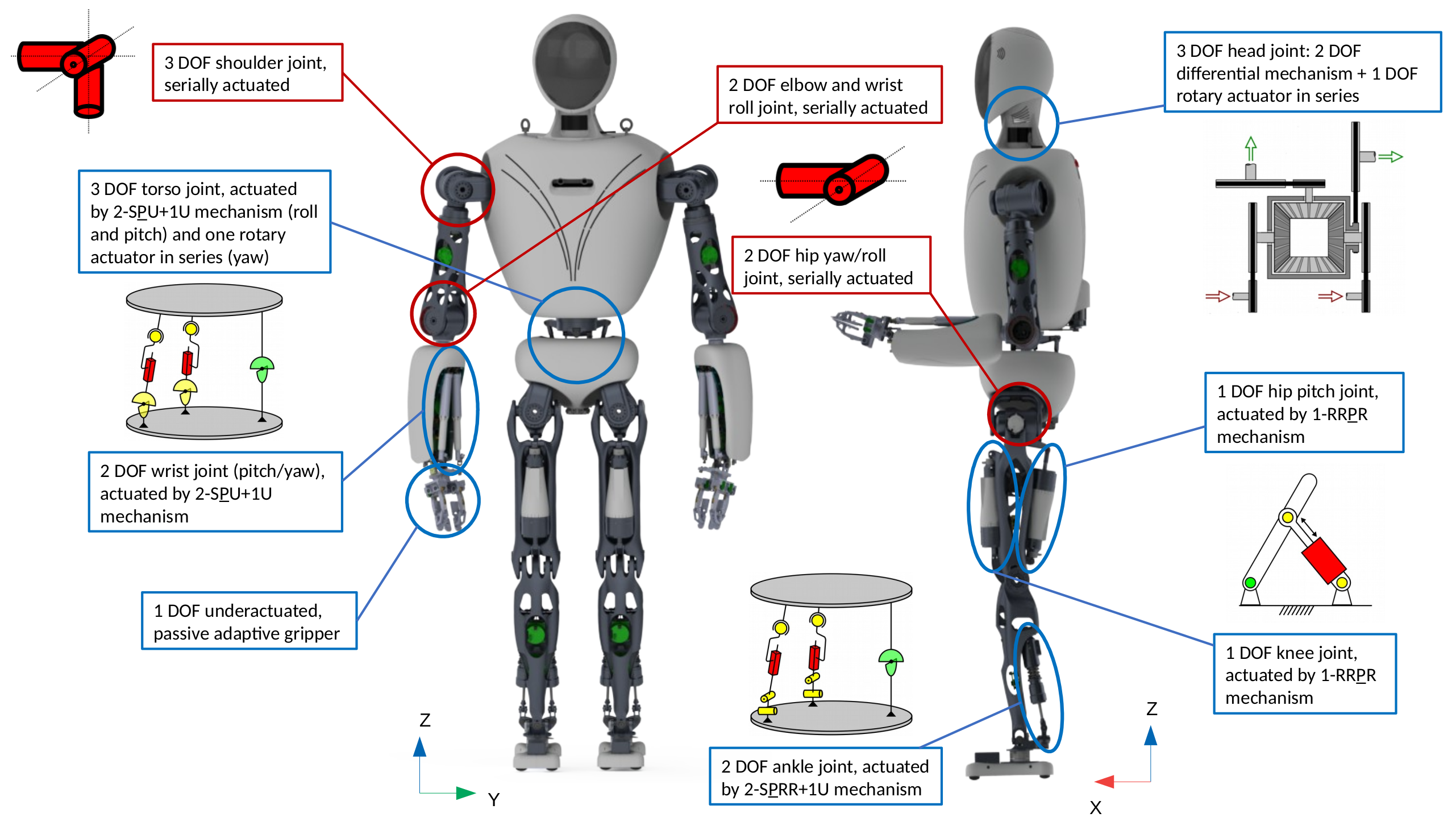
Last decades of humanoid research has shown that humanoids developed for high dynamic performance require a stiff structure and optimal distribution of mass~ inertial properties. Humanoid robots built with a purely tree type architecture tend to be bulky and usually suffer from velocity and force/torque limitations. This paper presents a novel series-parallel hybrid humanoid called RH5 which is 2 m tall and weighs only 62.5 kg capable of performing heavy-duty dynamic tasks with 5 kg payloads in each hand. The analysis and control of this humanoid is performed with whole-body trajectory optimization technique based on differential dynamic programming (DDP). Additionally, we present an improved contact stability soft-constrained DDP algorithm which is able to generate physically consistent walking trajectories for the humanoid that can be tracked via a simple PD position control in a physics simulator. Finally, we showcase preliminary experimental results on the RH5 humanoid robot.



Planning whole-body motions while taking into account the terrain conditions is a challenging problem for legged robots since the terrain model might produce many local minima. Our coupled planning method uses stochastic and derivatives-free search to plan both foothold locations and horizontal motions due to the local minima produced by the terrain model. It jointly optimizes body motion, step duration and foothold selection, and it models the terrain as a cost-map. Due to the novel attitude planning method, the horizontal motion plans can be applied to various terrain conditions. The attitude planner ensures the robot stability by imposing limits to the angular acceleration. Our whole-body controller tracks compliantly trunk motions while avoiding slippage, as well as kinematic and torque limits. Despite the use of a simplified model, which is restricted to flat terrain, our approach shows remarkable capability to deal with a wide range of non-coplanar terrains. The results are validated by experimental trials and comparative evaluations in a series of terrains of progressively increasing complexity.


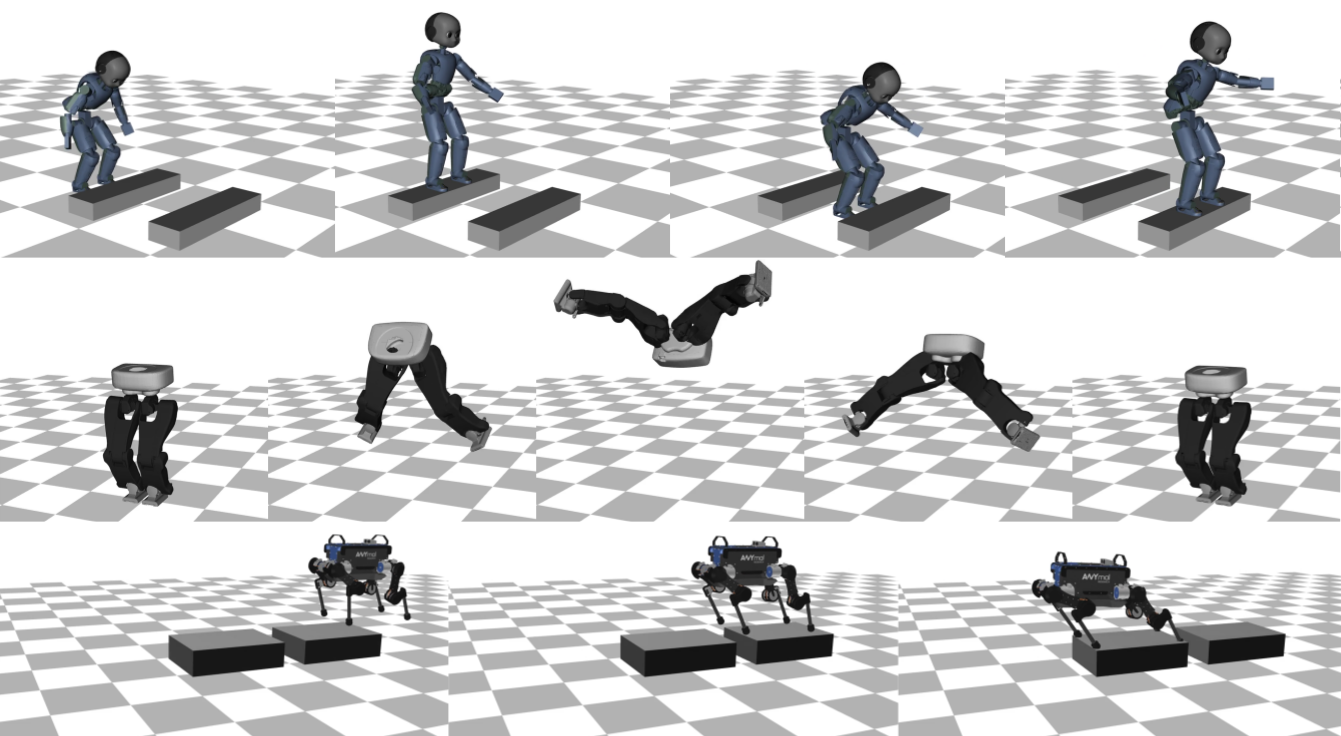
We introduce Crocoddyl (Contact RObot COntrol by Differential DYnamic Library), an open-source framework tailored for efficient multi-contact optimal control. Crocoddyl efficiently computes the state trajectory and the control policy for a given predefined sequence of contacts. Its efficiency is due to the use of sparse analytical derivatives, exploitation of the problem structure, and data sharing. It employs differential geometry to properly describe the state of any geometrical system, e.g. floating-base systems. Additionally, we propose a novel optimal control algorithm called Feasibility-driven Differential Dynamic Programming (FDDP). Our method does not add extra decision variables which often increases the computation time per iteration due to factorization. FDDP shows a greater globalization strategy compared to classical Differential Dynamic Programming (DDP) algorithms. Concretely, we propose two modifications to the classical DDP algorithm. First, the backward pass accepts infeasible state-control trajectories. Second, the rollout keeps the gaps open during the early ''exploratory'' iterations (as expected in multipleshooting methods with only equality constraints). We showcase the performance of our framework using different tasks. With our method, we can compute highly-dynamic maneuvers (e.g. jumping, front-flip) within few milliseconds.



In this paper, we propose a framework to build a memory of motion for warm-starting an optimal control solver for the locomotion task of a humanoid robot. We use HPP Loco3D, a versatile locomotion planner, to generate offline a set of dynamically consistent whole-body trajectory to be stored as the memory of motion. The learning problem is formulated as a regression problem to predict a single-step motion given the desired contact locations, which is used as a building block for producing multi-step motions. The predicted motion is then used as a warm-start for the fast optimal control solver Crocoddyl. We have shown that the approach manages to reduce the required number of iterations to reach the convergence from ∼9.5 to only ∼3.0 iterations for the single-step motion and from ∼6.2 to ∼4.5 iterations for the multi-step motion, while maintaining the solution’s quality.


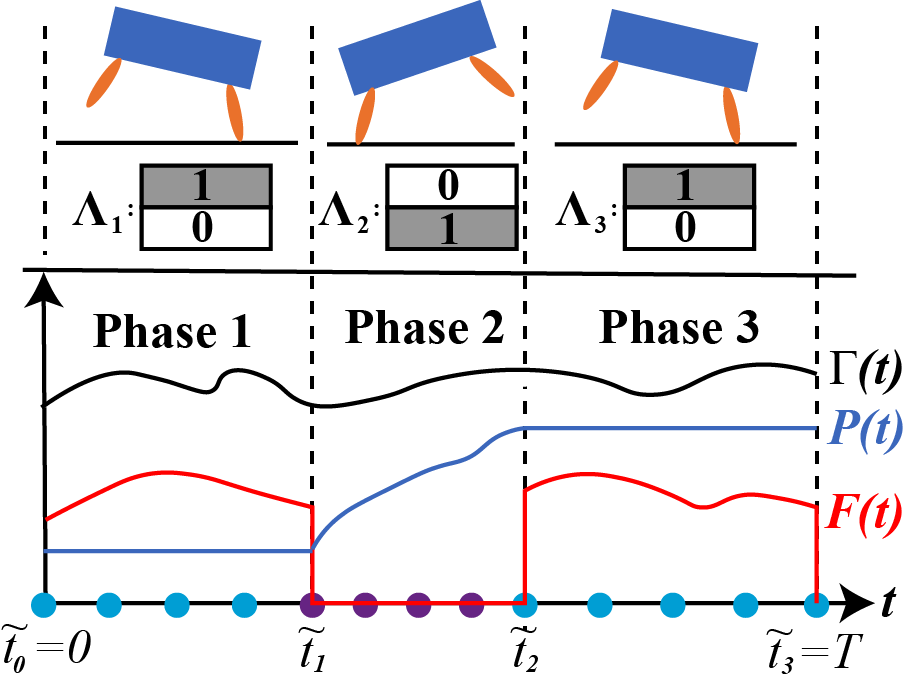
An important issue when synthesizing legged locomotion plans is the combinatorial complexity that arises from gait pattern selection. Though it can be defined manually, the gait pattern plays an important role in the feasibility and optimality of a motion with respect to a task. Replacing human intuition with an automatic and efficient approach for gait pattern selection would allow for more autonomous robots, responsive to task and environment changes. To this end, we propose the idea of building a map from task to gait pattern selection for given environment and performance objective. Indeed, we show that for a 2D half-cheetah model and a quadruped robot, a direct mapping between a given task and an optimal gait pattern can be established. We use supervised learning to capture the structure of this map in a form of gait regions. Furthermore, we propose to construct a warm-starting trajectory for each gait region. We empirically show that these warm-starting trajectories improve the convergence speed of our trajectory optimization problem up to 60 times when compared with random initial guesses. Finally, we conduct experimental trials on the ANYmal robot to validate our method.


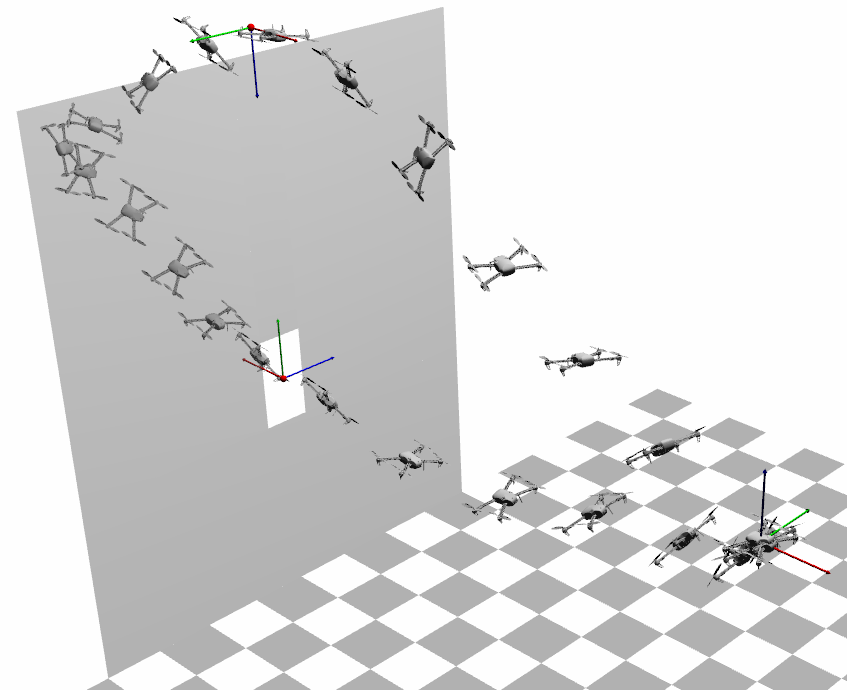
Recently, Differential Dynamic Programming (DDP) and other similar algorithms have become the solvers of choice when performing non-linear Model Predictive Control (nMPC) with modern robotic devices. The reason is that they have a lower computational cost per iteration when compared with off-the-shelf Non-Linear Programming (NLP) solvers, which enables its online operation. However, they cannot handle constraints, and are known to have poor convergence capabilities. In this paper, we propose a method to solve the optimal control problem with control bounds through a squashing function (i.e., a sigmoid, which is bounded by construction). It has been shown that a naive use of squashing functions damage the convergence rate. To tackle this, we first propose to add a quadratic barrier that avoids the difficulty of the plateau produced by the sigmoid. Second, we add an outer loop that adapts both the sigmoid and the barrier; it makes the optimal control problem with the squashing function converge to the original control-bounded problem. To validate our method, we present simulation results for different types of platforms including a multi-rotor, a biped, a quadruped and a humanoid robot.



This paper describes the implementation of a canonical motion generation pipeline guided by vision for a TALOS humanoid robot. The proposed system is using a multicontact planner, a Differential Dynamic Programming (DDP) algorithm, and a stabilizer. The multicontact planner provides a set of contacts and dynamically consistent trajectories for the Center-Of-Mass (CoM) and the Center-Of-Pressure (CoP). It provides a structure to initialize a DDP algorithm which, in turn, provides a dynamically consistent trajectory for all the joints as it integrates all the dynamics of the robot, together with rigid contact models and the visual task. Tested on Gazebo the resulting trajectory had to be stabilized with a state-of-the-art algorithm to be successful. In addition to testing motion generated from high specifications to the stabilized motion in simulation, we express visual features at Whole Body Generator level which is a DDP formulated solver. It handles non-linearities as the ones introduced by the projections of visual features expressed and minimized in the image plan of the camera.


We present experimental results using a passive whole-body control approach for quadruped robots that achieves dynamic locomotion while compliantly balancing the robot's trunk. We formulate the motion tracking as a quadratic program that takes into account the full robot rigid body dynamics, the actuation limits, the joint limits, and the contact interaction. We analyze the controller's robustness against inaccurate friction coefficient estimates and unstable footholds, as well as its capability to redistribute the load as a consequence of enforcing actuation limits. Additionally, we present practical implementation details gained from the experience with the real platform. Extensive experimental trials on the 90 kg hydraulically actuated quadruped robot validate the capabilities of this controller under various terrain conditions and gaits. The proposed approach is superior for accurate execution of highly dynamic motions with respect to the current state of the art.


The quality of the visual feedback can vary significantly on a legged robot that is meant to traverse unknown and unstructured terrains. The map of the environment, acquired with online state-of-the-art algorithms, often degrades after a few steps, due to sensing inaccuracies, slippage and unexpected disturbances. When designing locomotion algorithms, this degradation can result in planned trajectories that are not consistent with the reality, if not dealt properly. In this work, we propose a heuristic-based planning approach that enables a quadruped robot to successfully traverse a significantly rough terrain (e.g., stones up to 10 cm of diameter), in absence of visual feedback. When available, the approach allows also to exploit the visual feedback (e.g., to enhance the stepping strategy) in multiple ways, according to the quality of the 3D map. The proposed framework also includes reflexes, triggered in specific situations, and the possibility to estimate online an unknown time-varying disturbance and compensate for it. We demonstrate the effectiveness of the approach with experiments performed on our quadruped robot HyQ (85 kg), traversing different terrains, such as: ramps, rocks, bricks, pallets and stairs. We also demonstrate the capability to estimate and compensate for disturbances, showing the robot walking up a ramp while pulling a cart attached to its back.


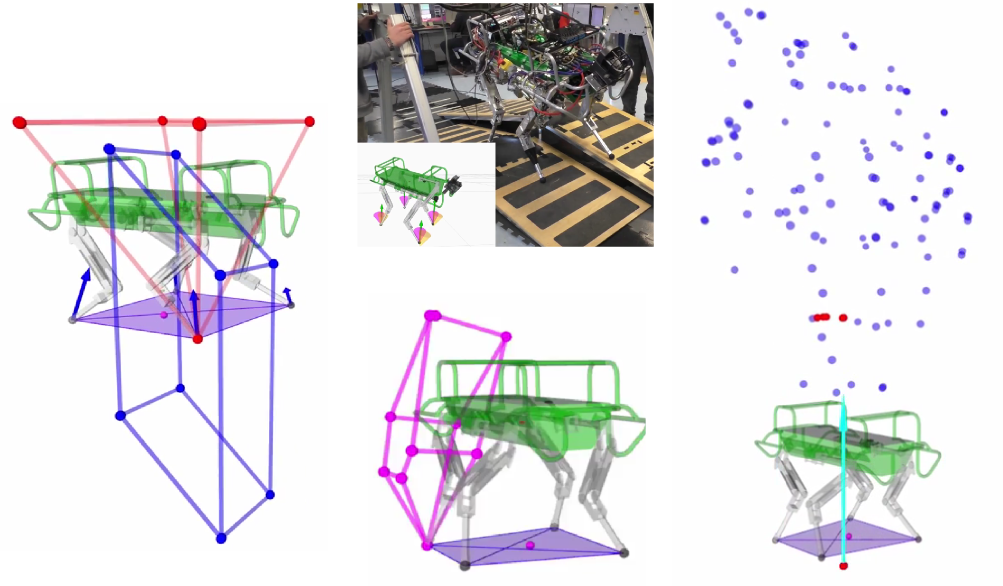
Motion planning in multicontact scenarios has recently gathered interest within the legged robotics community, however actuator force/torque limits are rarely considered. We believe that these limits gain paramount importance when the complexity of the terrains to be traversed increases. We build on previous research from the field of robotic grasping to propose two new six-dimensional bounded polytopes named the Actuation Wrench Polytope (AWP) and the Feasible Wrench Polytope (FWP). We define theAWP as the set of all the wrenches that a robot can generate while considering its actuation limits. This considers the admissible contact forces that the robot can generate given its current configuration and actuation capabilities. The Contact Wrench Cone (CWC) instead includes features of the environment such as the contact normal or the friction coefficient. The intersection of the AWP and of the CWC results in a convex polytope, the FWP, which turns out to be more descriptive of the real robot capabilities than existing simplified models, while maintaining the same compact representation. We explain how to efficiently compute the vertex-description of the FWP that is then used to evaluate a feasibility factor that we adapted from the field of robotic grasping. This allows us to optimize for robustness to external disturbance wrenches. Based on this, we present an implementation of a motion planner for our quadruped robot HyQ that provides online Center of Mass trajectories that are guaranteed to be statically stable and actuation-consistent.



A common strategy to generate efficient locomotion movements is to split the problem into two consecutive steps: the first one generates the contact sequence together with the centroidal trajectory, while the second step computes the whole-body trajectory that follows the centroidal pattern. While the second step is generally handled by a simple program such as an inverse kinematics solver, we propose in this paper to compute the whole-body trajectory by using a local optimal control solver, namely Differential Dynamic Programming (DDP). Our method produces more efficient motions, with lower forces and smaller impacts, by exploiting the Angular Momentum (AM). With this aim, we propose an original DDP formulation exploiting the Karush- Kuhn-Tucker constraint of the rigid contact model. We experimentally show the importance of this approach by executing large steps walking on the real HRP-2 robot, and by solving the problem of attitude control under the absence of external contact forces.



Traditional motion planning approaches for multilegged locomotion divide the problem into several stages, such as contact search and trajectory generation. However, reasoning about contacts and motions simultaneously is crucial for the generation of complex whole-body behaviors. Currently, coupling theses problems has required either the assumption of a fixed gait sequence and flat terrain condition, or nonconvex optimization with intractable computation time. In this letter, we propose a mixed-integer convex formulation to plan simultaneously contact locations, gait transitions, and motion, in a computationally efficient fashion. In contrast to previous works, our approach is not limited to flat terrain nor to a prespecified gait sequence. Instead, we incorporate the friction cone stability margin, approximate the robot's torque limits, and plan the gait using mixed-integer convex constraints. We experimentally validated our approach on the HyQ robot by traversing different challenging terrains, where nonconvexity and flat terrain assumptions might lead to suboptimal or unstable plans. Our method increases the motion robustness while keeping a low computation time.


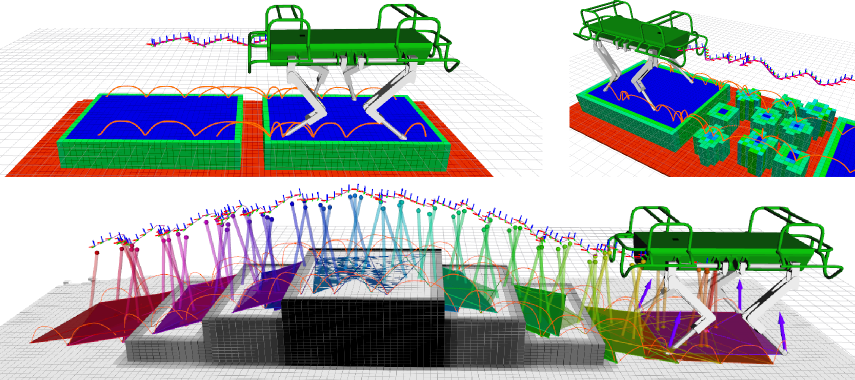
We present a trajectory optimization framework for legged locomotion on rough terrain. We jointly optimize the center of mass motion and the foothold locations, while considering terrain conditions. We use a terrain costmap to quantify the desirability of a foothold location. We increase the gait's adaptability to the terrain by optimizing the step phase duration and modulating the trunk attitude, resulting in motions with guaranteed stability. We show that the combination of parametric models, stochastic-based exploration and receding horizon planning allows us to handle the many local minima associated with different terrain conditions and walking patterns. This combination delivers robust motion plans without the need for warm-starting. Moreover, we use soft-constraints to allow for increased flexibility when searching in the cost landscape of our problem. We showcase the performance of our trajectory optimization framework on multiple terrain conditions and validate our method in realistic simulation scenarios and experimental trials on a hydraulic, torque controlled quadruped robot.


Biological limbs normally come in pairs: mammals have four, insects have six, arachnids have eight, and centipedes have one pair of legs per body segment. This work attempts to interpret the biological method of controlling paired legs (here treated as dual-arms) in opposite and adjacent pairs to achieve a holistic controller of a large four-legged animal (here treated as a combined four-arm robot). A modular relative Jacobian controls a dual-arm as a single manipulator with a single end-effector, and is expressed in terms of the Jacobians of each of the stand-alone manipulators. In this work, the two opposite pairs of legs are treated as single end-effector dual-arms, and then these two dual-arms are combined together to form a single end-effector four-arm robot. The four-arm controller uses the same principle as a single end-effector controller of a dual-arm, and thus results into a single end-effector controller of a four-arm. A modular relative Jacobian of the four arms is derived. Gazebo simulation results are shown for two gait patterns of a four-legged animal, namely, pacing and trotting.



Most animal and human locomotion behaviors for solving complex tasks involve dynamic motions and rich contact interaction. In fact, complex maneuvers need to consider dynamic movement and contact events at the same time. We present a hierarchical trajectory optimization approach for planning dynamic movements with unscheduled contact sequences. We compute whole-body motions that achieve goals that cannot be reached in a kinematic fashion. First, we find a feasible CoM motion according to the centroidal dynamics of the robot. Then, we refine the solution by applying the robot's full-dynamics model, where the feasible CoM trajectory is used as a warm-start point. To accomplish the unscheduled contact behavior, we use complementarity constraints to describe the contact model, i.e. environment geometry and non-sliding active contacts. Both optimization phases are posed as Mathematical Program with Complementarity Constraints (MPCC). Experimental trials demonstrate the performance of our planning approach in a set of challenging tasks.


We present a framework for dynamic quadrupedal locomotion over challenging terrain, where the choice of appropriate footholds is crucial for the success of the behaviour. We build a model of the environment on-line and on-board using an efficient occupancy grid representation. We use Any-time-Repairing A* (ARA*) to search over a tree of possible actions, choose a rough body path and select the locally-best footholds accordingly. We run a n-step lookahead optimization of the body trajectory using a dynamic stability metric, the Zero Moment Point (ZMP), that generates natural dynamic whole-body motions. A combination of floating-base inverse dynamics and virtual model control accurately executes the desired motions on an actively compliant system. Experimental trials show that this framework allows us to traverse terrains at nearly 6 times the speed of our previous work, evaluated over the same set of trials.



We present a legged motion planning approach for quadrupedal locomotion over challenging terrain. We decompose the problem into body action planning and footstep planning. We use a lattice representation together with a set of defined body movement primitives for computing a body action plan. The lattice representation allows us to plan versatile movements that ensure feasibility for every possible plan. To this end, we propose a set of rules that define the footstep search regions and footstep sequence given a body action. We use Anytime Repairing A* (ARA*) search that guarantees bounded suboptimal plans. Our main contribution is a planning approach that generates on-line versatile movements. Experimental trials demonstrate the performance of our planning approach in a set of challenging terrain conditions. The terrain information and plans are computed on-line and on-board.

